Hypothesis Testing¶
Overview¶
Statisticians answer questions in a strange manner. Instead of definite YES or NO they specify a probability to YES (and one minus this probability to NO).
- Did this person rob a bank?
- Let me be correct at least $990$ times out of $100$. Then I answer NO.
People seem that they make a discovery and ask statisticians to verify whether this is a discovery indeed. Statistician verify whether observations fit typical processes. In other words, how extraordinary the data are against a typical process. Then the question about the specification of extraordinary things rises. If the statistician agrees to be wrong rarely, they call an event extraordinary only in exceptional case. Otherwise, rather normal events can be called extraordinary. This subject is discussed in details below. Required computer codes are provided.
General Framework¶
- The goal of a statistical test is to make a statement about the agreement between the observed data and theoretical probabilities
- The statement is referred to as a hypothesis
- Typically, one distinguishes between two hypotheses
- Null hypothesis is the boring stuff: it assumes that nothing interesting occurs
- Alternative hypotheses is related to the observation of a real phenomenon. A researcher aims to decide whether this observation differs from the boring stuff
- The hypothesis could specify the probability density function $f(x)$ from which the observations are obtained.
- If the hypothesis determine $f(x)$ fully than it is simple.
- If the form of the $\texttt{pdf}$ is defined but not the values of at least one free parameter $\theta$, then $f(x;\theta)$ is called a composite hypothesis. We will focus on simple hypotheses now
- Measured values: $\mathbf{x} = (x_1, \ldots, x_n)$ form a sample
- $f(\mathbf{x} | H)$ denotes the probability distribution function that describes the vector of random variables $(X_1, \ldots, X_n)$ or consequent $n$ observations of the same random variable $X$ under some hypothesis
- When the hypothesis is specified, its name is used, f.~e., $f(\mathbf{x} | H_0)$ or $f(\mathbf{x} | H_1)$.
- The hypothesis $H$ could also indicate a random variable, but the notation $f(\mathbf{x})$ still works.
- To discriminate between the hypotheses, we choose an appropriate statistics $T(\mathbf{x})$
- Example: let the chosen statistics be one-dimensional, $T(\mathbf{x}) \in \mathbb{R}$. Its probability distribution function is $g(t | H_0)$ if $H_0$ is true and $g(t | H_1)$ if $H_1$ is true.
- Decision: Reject, if the observed value $> t_{\text{cut}}$
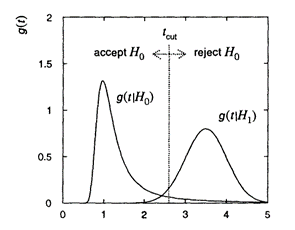 |
$\newcommand{\Prob}[1]{\mathsf{P}\{#1\}}$ $\newcommand{\Exp}{\mathbf{E}\,}$ $\newcommand{\Var}{\mathbf{Var}\,}$
- $H_0$: the observations are taken from the normal random variable $X$ with the mean $\mu_0$ (the normality is assumed / known; the question is only about the mean)
- Two opportunities for the alternative:
- $H_1$: $\mu = \Exp X > \mu_0$ (one-sided)
- $H_1$: $\mu = \Exp X \ne \mu_0$ (two-sided)
- Statistics, as a random variable that depends on the independent normal random variables $X_1$, $\ldots$, $X_n$ (identical to $X$) with unknown $\Exp X_j = \mu$ and known $\Var X_j = s^2$, $j=1, \ldots, n$, $$ T = \frac{(X_1+\ldots+X_n)/n - \mu_0}{\sqrt{s^2/n}} $$
$\newcommand{\Prob}[1]{\mathsf{P}\{#1\}}$
Question: What is the distribution of $T$, provided $H_0: \mu = \mu_0$?
* $T\sim \mathbf{N}(0, 1)$
- Let's deal with the one-sided alternative $\mu > \mu_0$. Then reject $H_0$ if the observed value of the statistics $$ t = \frac{\bar{\mathbf{x}}-\mu_0}{\sqrt{s^2/n}} > t_{\text{cut}} $$
- The choice of the critical value $t_{\text{cut}}$ depends on the fact how confident we are rejecting the hypothesis.
- Assume that you agree to be wrong rejecting $H_0$ on average once out of $1000$ trials. Then define $\alpha = 0.001$ and choose $t_{\text{cut}}$ based on the equation $\Prob{T > t_{\text{cut}}} = \alpha$
$\newcommand{\Prob}[1]{\mathsf{P}\{#1\}}$
- In our equation $$ \Prob{T > t_{\text{cut}}} = \alpha $$ $\alpha$ is the significance level and $t_{\text{cut}}$ is the $(1-\alpha)$-quantile.
Question: If you agree to maintain the rejection on a weaker basis in what direction will you change the significance level?
- You'll make it larger. What will occur with the critical value?
- You can reverse the above story. I observed the data. What is the probability to find a more extreme value under the hypothesis $H_0$?
- This probability is called $p$-value.
- $p$$ = \Prob{T > t}$, where
$\quad\displaystyle t = \frac{\bar{\mathbf{x}}-\mu_0}{\sqrt{s^2/n}}$
$\newcommand{\Prob}[1]{\mathsf{P}\{#1\}}$
- Extreme values cover both tails
- Given the confidence level $\alpha$,
- In our case, the distribution is symmetrical,
and
$$ \Prob{T > t_{\text{cut}}} = \frac{\alpha}{2} \Longleftrightarrow 1-\Phi(t_{\text{cut}}) = \frac{\alpha}{2} $$$$ t_{\text{cut}} = \Phi^{-1}\left(1-\frac{\alpha}{2}\right) $$Statistical Errors¶
- An incorrect decision is an error
- A false rejection of the null hypothesis $H_0$ (rejecting $H_0$ when $H_0$ is true) is a Type I error
- A false acceptance of $H_0$ (accepting $H_0$ when $H_0$ is false) is a Type II error
| Accept $H_0$ | Reject $H_0$ | |
| $H_0$ true | Correct Decision | Type I Error |
| $H_1$ true | Type II Error | Correct Decision |
- Research question: Does an early childhood education affect the adult wage earnings?
- Two groups of adult respondents (with early childhood education and the control group). What are relevant criteria to select the groups?
- Outcome: the distribution of the salaries within both groups
- $H_0$: the means in the samples are identical
- $H_1$: the mean in the group corresponding to the early childhood education is larger
$\newcommand{\Prob}[1]{\mathsf{P}\{#1\}}$
- The size of a hypothesis test is the probability of a Type I error
- The power of the test is the complement of the probability of a Type II error
$\newcommand{\Prob}[1]{\mathsf{P}\{#1\}}$ $\newcommand{\Exp}{\mathbf{E}\,}$ $\newcommand{\Var}{\mathbf{Var}\,}$
Mean of normal sampling with unknown variance $\sigma^2$
$H_0$: the observations are taken from the normal random variable $X$ with the mean $\mu_0$ (the normality is assumed / known; the question is only about the mean)
Two opportunities for the alternative:
$H_1$: $\mu = \Exp X > \mu_0$ (one-sided)
$H_1$: $\mu = \Exp X \ne \mu_0$ (two-sided)
Analogiously to the earlier example
Statistics, as a random variable that depends on the independent normal random variables $X_1$, $\ldots$, $X_n$ (identical to $X$) with unknown $\Exp X_j = \mu$ and unknown $\Var X_j = \sigma^2$, $j=1, \ldots, n$, $$ T = \frac{(X_1+\ldots+X_n)/n - \mu}{\sqrt{s^2/n}} $$
$\newcommand{\Prob}[1]{\mathsf{P}\{#1\}}$
Question: What is the distribution of $T$, provided $H_0: \mu = \mu_0$?
- $T$ is given by Student's $t_{n-1}$-distribution with $n-1$ degree of freedom, where $n$ is the number of observations; it is asymptotically normal, i.~e., $t_{n-1}\sim \mathbf{N}(0, 1)$ as $n\to\infty$
- Let's deal with the one-sided alternative $\mu > \mu_0$. Then reject $H_0$ if the observed value of the statistics
where $\sigma$ is the sample standard deviation and the probability $\Prob{T > t_{\text{cut}}} = \alpha$ is computed based on Student's distribution function $G_{n-1}$ with $n-1$ degrees of freedom:
$$ 1-G_{n-1}(t_{\text{cut}}) = \alpha, \quad t_{\text{cut}} = G_{n-1}^{-1}(1-\alpha) $$- Two-sided hypothesis:
As an example let us generate a sample from the normal random variable with the expected value of $1.5$, the standard deviation of $2$, and the size of $100$
from scipy.stats import norm
x = norm.rvs(loc=1.5, scale=2, size=100, random_state=1)
Task: test the hypothesis that $x$ is from the normal distribution with $\mu=1.55$ and unknown standard deviation against the two-sided alternative. Significance level is $0.01$. Report the $p$-value.
import numpy as np
from scipy.stats import t
mu0 = 1.55
alpha = 0.01 #significance level
mu = np.mean(x) #sample mean
n = len(x)
sigma = np.std(x)*np.sqrt(n/(n-1)) #corrected standard deviation
t_stat = (mu - mu0) / (sigma / np.sqrt(n)) #Student statistics
cdf = t.cdf(t_stat, n-1)
if cdf > 0.5:
pvalue = (1-cdf)*2
else:
pvalue = cdf*2
print('sample mean = {:.3f};'.format(mu), 'statistics = ', t_stat, 'p-value = {:.3f}'.format(pvalue))
cutoff_low = t.ppf(alpha/2, n-1) # \int_{-\infty}^{cutoff_low} t(x) dx = \alpha/2
cutoff_high = t.ppf(1-alpha/2, n-1) # \int_{cutoff_high}^{+\infty} t(x) dx = \alpha/2
print('significance level = ', alpha, '; cut-offs: {:.3f} and {:.3f}'.format(cutoff_low, cutoff_high),
'; reject?', t_stat < cutoff_low or t_stat > cutoff_high)
Conclusion: With our data, we are OK with the null hypothesis, which is $\mu_0 = 0.55$, at the prescribed significance level. Mind that $p$-value is rather large so that we would not agree the null hypothesis had the significance level were even larger.
Do not forget that the true value of the mean is $\mu = 0.5$.
$\newcommand{\Prob}[1]{\mathsf{P}\{#1\}}$
- Power of the test increases in
- the significance level $\alpha$
- the true value of the mean $\mu$
- but decreases in the standard deviation $\sigma$
- does the case $\sigma\to 0$ correspond to your intuition?
- the graph is obtained with some fixed value of $\mu$
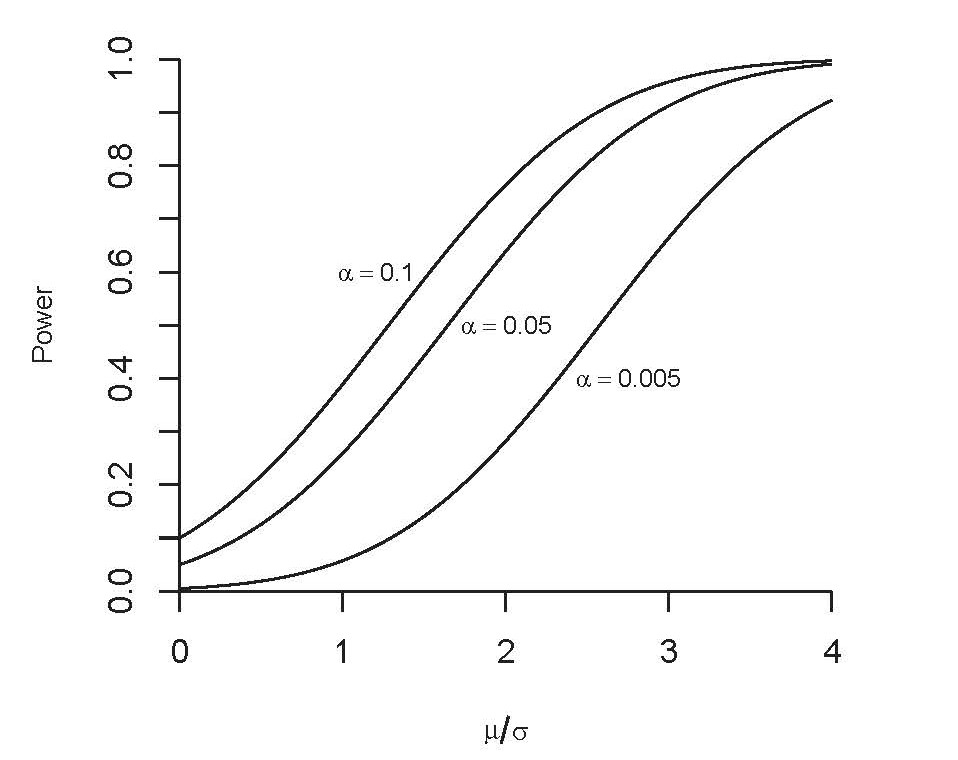 |
Example: Does first baby come later?¶
The example including the database and some codes are taken from handbook "Statistical Thinking"
Anecdotical evidence
“My two friends that have given birth recently to their first babies, BOTH went almost 2 weeks overdue before going into labour or being induced.”
“My first one came 2 weeks late and now I think the second one is going to come out two weeks early!!”
“I don’t think that can be true because my sister was my mother’s first and she was early, as with many of my cousins.”
Small number of observations: If the gestation period is longer for first babies, the difference is probably small compared to the natural variation. In that case, we might have to compare a large number of pregnancies to be sure that a difference exists.
Selection bias: People who join a discussion of this question might be interested because their first babies were late. In that case the process of selecting data would bias the results.
Confirmation bias: People who believe the claim might be more likely to contribute examples that confirm it. People who doubt the claim are more likely to cite counterexamples.
Inaccuracy: Anecdotes are often personal stories, and often misremembered, misrepresented, repeated inaccurately, etc.
So how can we do better?
DATA: U.S. Centers for Disease Control and Prevention (CDC) have conducted the National Survey of Family Growth (NSFG)
- to use the data one must agree to comply with general rules (basically, not try to identify people whose data are recorded)
for i in range(5):
rec = table.records[i]
outcome = rec.outcome
birthord = rec.birthord
caseid = rec.caseid
nbrnaliv = rec.nbrnaliv
babysex = rec.babysex
prglength = rec.prglength
print(outcome, birthord, caseid, nbrnaliv, babysex, prglength)
We can formulate two different questions
- $H_0$: the mean expectation of the first baby is the same as that of the other babies against one-sided alternative $H_1$: the mean expectation of the first baby is larger than that of the other babies
- More general formulation
$H_0$: the probability distribution of the delivery expectation is the same for the first and other babies
against two-sided alternative that the distributions are different.
Here we somewhat avoid the initial formulation of the problem, skipping the rumor that the first pregnancy is longer.
The second problem is solved below. The first formulation is left to the reader; the required rule is formulated below at the paragraph that compares the means of two samples
Attention: change in the sample
- We remember that our data exhibits strange values related to the first weeks
- Let us focus on the sub-sample that does not include the data about the first weeks as we have already done
Repetition (see the first lecture)
import numpy as np
import sys
sys.path.insert(0, "..")
from lib import survey
table = survey.Pregnancies()
table.ReadRecords()
print ('Number of pregnancies', len(table.records))
#Read pregnancy length from the database and save to prglength
prglength = []
for rec in table.records:
prglength.append(rec.prglength)
#Split the pregnancy length itno two two files with the first and other pregnancies
prglength_first = []
prglength_other = []
for rec in table.records:
if rec.birthord == 1:
prglength_first.append(rec.prglength)
else:
prglength_other.append(rec.prglength)
Adjustment of the built-in histograms and empirical distribution functions
Library functions draw rectangles that are not always useful
#Empirical probability density function
#returns two arrays: centers of the bins and pdf-values
def pdf_my(array, n_bins = 10, arr_min = [], arr_max = []):
array = np.array(array)
if np.size(arr_min) == 0:
arr_min = min(array)
if np.size(arr_max) == 0:
arr_max = max(array)
if n_bins == 0:
raise Exception('At least 1 bin required')
else:
x = []
y = []
gap = (arr_max - arr_min) / n_bins
for i in range(n_bins):
x.append(arr_min + (0.5 + i) * gap)
y.append(0)
n_els = 0
for arr in array:
cur = int(math.floor((arr - arr_min) / gap))
if cur >= 0 and cur < n_bins:
y[cur] += 1
n_els += 1
if n_els > 0:
for cur in range(len(y)):
y[cur] = y[cur] / n_els / gap
return x, y
#plot histogram and return the points at the middle of the top side of the rectangle
def hist_my_rectangle(array, n_bins = 10):
res = plt.hist(array, n_bins)
xx = res[1] #xx[] gives the endpoints of the bins, we need their centers
y = res[0]
# xx -> x
x = []
for i in range(len(xx)-1):
x.append((xx[i] + xx[i+1]) / 2)
return x, y
Let's draw the histogram with and without rectangles
import matplotlib.pyplot as plt
x, y = hist_my_rectangle(prglength, 10)
plt.plot(x, y)
plt.show()
Attention: outliers
Are we interested in the large yellow values?
#ignore values outside [week_frst, week_last]
def newarr(arr, week_frst, week_last):
x1 = []
for x in arr:
if x >= week_frst and x <= week_last:
x1.append(x)
return x1
import matplotlib.pyplot as plt
weeks = [27, 42]
#weeks2 = [28, 41] #you can try other values and justify the stability of the result
x1 = newarr(prglength_first, weeks[0], weeks[1])
x2 = newarr(prglength_other, weeks[0], weeks[1])
n_bins=weeks[1]-weeks[0]
x_first, y_first = pdf_my(x1, n_bins=n_bins,
arr_min=weeks[0]-0.5, arr_max=weeks[1]+0.5)
plt.plot(x_first, y_first, marker = 'o', label = 'quatntity: first')
x_other, y_other = pdf_my(x2, n_bins=n_bins,
arr_min=weeks[0]-0.5, arr_max=weeks[1]+0.5)
plt.plot(x_other, y_other, marker = 'o', label = 'quatntity: other')
plt.legend()
plt.show()
print(x1[1:30])
print(x2[1:30])
Some words about probability distribution function
Questions:
What are properties of the cumulative distribution functions?
Let's sketch the cumulative distribution function $F(x)$ if the probability density is given.
The sides of a coin are labeled with $0$ and $1$; $X$ is the label observed on the coin. What is the probability distribution function of $X$
$F(x)$ is the cumulative distribution function of $X$. What is the cumulative distribution function of $Y = 2X+3$? $Z=X^2$
* $$\mathbb{P}\{X^2 < z\} =
\begin{cases}
\mathbb{P}\{X \in (-\sqrt{z}, \sqrt{z})\} & \text{if $z > 0$}
\\
0 & \text{otherwise}
\end{cases}
=
\begin{cases}
F(\sqrt{z}) - F(-\sqrt{z}) & \text{if $z > 0$}
\\
0 & \text{otherwise}
\end{cases}
$$
We are using the test on the equality of two means without any explanations
#Details below
import numpy as np
from scipy.stats import t
#Testing the equality of two means at level alpha
def test_equal_means(m1, s1, n1, m2, s2, n2, alpha):
#print(m1, m2)
s = np.sqrt(s1 ** 2 / n1 + s2 ** 2 / n2)
tstar = (m1 - m2) / s
df = (s1 ** 2 / n1 + s2 ** 2 / n2) ** 2 / \
(s1 ** 4 / (n1**2*(n1-1)) + s2 ** 4 / (n2**2*(n2-1)))
print(tstar, round(df))
prb1t = 1 - t.cdf(np.abs(tstar), df)
prb2t = (1 - t.cdf(np.abs(tstar), df)) * 2
print('Probability_2_tailed = ', prb2t)
return prb1t >= alpha, prb2t >= alpha
#Compute the probability that the first and the other babies come
#after approximately the same expectation
alpha = 0.05
m1 = np.mean(x1)
s1 = np.std(x1)
n1 = len(x1)
m2 = np.mean(x2)
s2 = np.std(x2)
n2 = len(x2)
print(test_equal_means(m1, s1, n1, m2, s2, n2, alpha))
t-test verifying the identity of distributions
from scipy.stats import ttest_ind
ttest_ind(x1, x2)
In our story with the first baby, the comparison of the means was performed just to give the example of the method. We could first apply the Kolomogorov-Smirnov test, discussed above.
The usage is explained here
To recall, we will reject the null hypothesis in favor of the alternative if the p-value is less than the confidence level (chosen before the test performence).
from scipy.stats import ks_2samp
cmp_xy = ks_2samp(x1, x2, alternative='two-sided')
print('Output', cmp_xy)
print('Probability that the observed deviation obtained with identical distributions: ',
format(cmp_xy[1], '.3e'))
significance_level = 0.05
print(f'Reject the coincidence of the distributions at level {significance_level}:',
cmp_xy[1] < significance_level)
Question:
If the research question is whether the first baby comes earlier, what is a correct alternative in the above method?
* alternative='less'
Research question: In previous years, 52% of parents believed that electronics and social media was the cause of their teenager’s lack of sleep. Do more parents today believe that their teenager’s lack of sleep is caused due to electronics and social media?
Population: Parents with a teenager (age 13–18)
Parameter of Interest: $\nu$ (proportion)
Null Hypothesis: $\nu = 0.52$
Alternative Hypothesis: $\nu > 0.52$ (note that this is a one-sided test)
Data: 1018 people were surveyed. $56\%$ of those who were surveyed believe that their teenager’s lack of sleep is caused due to electronics and social media.
Approach: Single group proportion uses z-statistic test. We use theproportions_ztest() function from the Statsmodels package. Note the argument alternative="larger" indicating a one-sided test. The function returns two values - the z-statistic and the corresponding $p$-value.
#source: https://towardsdatascience.com/demystifying-hypothesis-testing-with-simple-python-examples-4997ad3c5294
import statsmodels.api as sm
import numpy as np
import matplotlib.pyplot as plt
n = 1018
pnull = .52
phat = .56
sm.stats.proportions_ztest(phat * n, n, pnull, alternative='larger')
Conclusion: Since the calculated p-value (~0.005) of the z-test is pretty small, we can reject the Null hypothesis that the percentage of parents, who believe that their teenager’s lack of sleep is caused due to electronics and social media, is as same as previous years’ estimate i.e. 52%.\ Although we do not accept the alternative hypothesis, this informally means that there is a good chance of this proportion being more than 52%.
Difference in Population Proportions¶
Research Question Is there a significant difference between the population proportions of parents of black children and parents of Hispanic children who report that their child has had some swimming lessons?
Populations: All parents of black children age 6-18 and all parents of Hispanic children age 6-18
Parameter of Interest: $p1 - p2$, where $p1 = \texttt{black}$ and $p2 = \texttt{hispanic}$
Null Hypothesis: $p1 - p2 = 0$. Alternative Hypthosis: $p1 - p2 \neq 0$
Data:
247 Parents of Black Children. 36.8% of parents report that their child has had some swimming lessons.
308 Parents of Hispanic Children. 38.9% of parents report that their child has had some swimming lessons.
Use of ttest_ind() from statsmodels.
Difference in population proportion needs the t-test. Also, the population follow a binomial distribution here. We can just pass on the two population quantities with the appropriate binomial distribution parameters to the t-test function.
The function returns three values: (a) test statisic, (b) p-value of the t-test, and (c) degrees of freedom used in the t-test.
n1 = 247
p1 = .37
n2 = 308
p2 = .39
population1 = np.random.binomial(1, p1, n1)
population2 = np.random.binomial(1, p2, n2)
sm.stats.ttest_ind(population1, population2)
Conclusion $p$-value is large, the null hypothesis is not rejected. The proportions are likely to be the same.\ Let us increase the number of population
n1 = 10000
p1 = .37
n2 = 10000
p2 = .39
population1 = np.random.binomial(1, p1, n1)
population2 = np.random.binomial(1, p2, n2)
sm.stats.ttest_ind(population1, population2)
Now the $p$-value is significantly smaller. The exact value varies from one run to another but, as a rule, remains small.
Are the samples from the same probability distribution?¶
import numpy as np
from scipy.stats import ttest_ind
v1 = np.random.normal(size=100)
v2 = np.random.normal(size=100)
The samples are obtained from the same distribution. We check it statisticaly.
Find if the samples v1 and v2 are from the same distribution
res = ttest_ind(v1, v2)
print(res)
Criterion: p_value > significance_level
Are two means equal?¶
If the samples are not small, the probability distribution can be arbitrary (normal, in the opposite case).
Notation:
$\bar{x}_i$, $s_i$, $n_i$ are the mean, the standard deviation, and the number of sample $i$.
Pay attention: the population standard deviation is unknown; we use its estimate.
Compute the statistics
$$
t^* = \frac{\bar{x}_1 - \bar{x}_2}{s},
$$
where
$$
s = \sqrt{\frac{s_1^2}{n_1} + \frac{s_2^2}{n_2}}.
$$
According to secret knowledge, this statistics $s$ follows the Student distribution ($t$-distribution) with $df$ degrees of freedom,
where
$$
df = \frac{\left(\frac{s_1^2}{n_1} + \frac{s_2^2}{n_2}\right)^2}{\frac{s_1^4}{(n_1-1)n_1^2} + \frac{s_2^4}{(n_2-1)n_2^2}}.
$$
You are assumed to test the hypothesis at a given significance level $\alpha$. Find the critical value $q_{\alpha}$ at the corresponding table (against two-sided alternative).
If $|t^*| > q_{\alpha}$,
which means that the computed values is an extreme, i.e., occurs too rare (the fraction of their occurrence is less than $\alpha$) under the null hypothesis (about the equality of the means),
reject the null hypothesis, i.e., say that the means are not equal.
If $|t^*| \le q_{\alpha}$,
you cannot reject the hypothesis and you have in mind the means are likely to be equal.
Alternatively,
compute the probability $t > |t^*|$, where $t$ is the $t$-distribution with $df$ degrees of freedom, which is $1 - F_t(x) = \mathbf{Prob}\{t > X\}$, and divide is by $2$.
import numpy as np
from scipy.stats import t
#Testing the equality of two means at level alpha
def test_equal_means(m1, s1, n1, m2, s2, n2, alpha):
#print(m1, m2)
s = np.sqrt(s1 ** 2 / n1 + s2 ** 2 / n2)
tstar = (m1 - m2) / s
df = (s1 ** 2 / n1 + s2 ** 2 / n2) ** 2 / \
(s1 ** 4 / (n1**2*(n1-1)) + s2 ** 4 / (n2**2*(n2-1)))
print(tstar, round(df))
prb1t = 1 - t.cdf(np.abs(tstar), df)
prb2t = (1 - t.cdf(np.abs(tstar), df)) * 2
print('Probability_2_tailed = ', prb2t)
return prb1t >= alpha, prb2t >= alpha
Kolomogorov-Smirnov test¶
The test varifies whether the sample follows the distribution
from scipy.stats import kstest
np.random.seed(1) # set random seed to get the same result
v = np.random.normal(size=100)
u = np.random.normal(0, 1, 1000)
w = [-1, 1, 0, 0, 0, 0]
res_v = kstest(v, 'norm')
res_w = kstest(w, 'norm')
print(res_v)
print(res_w)
Conclusion The decision reject the null hypothesis (it is likely that the sample v is not normal if $p$ is less some pre-defined level of significance
Two identical normal distributions¶
rng = np.random.RandomState(1)
x = rng.rand(100) #Uniform distribution on [0, 1]
y = rng.rand(100)
print(np.mean(x), np.mean(y))
print(test_equal_means(np.mean(x), np.std(x), len(x),\
np.mean(y), np.std(y), len(y), 0.05))
Two different normal distributions¶
import numpy.random as random
x = []
y = []
for i in range(1000):
x.append(random.normal(0, 1))
y.append(random.normal(0.1, 1))
print('Means', '{:.3f}'.format(np.mean(x)), \
'{:.3f}'.format(np.mean(y)))
print('STDs', '{:.3f}'.format(np.std(x)),\
'{:.3f}'.format(np.std(y)))
print('Sample size', len(x), len(y))
df = (np.std(x) ** 2 / len(x) + np.std(y) ** 2 / len(y)) ** 2 / \
(np.std(x) ** 4 / (len(x)**2*(len(x)-1)) + \
np.std(y) ** 4 / (len(y)**2*(n2-1)))
print('Degree of freedom', df)
print(test_equal_means(np.mean(x), np.std(x), len(x),\
np.mean(y), np.std(y), len(y), 0.05))

